Partie théorique

Chapitre 1 – Diviseurs et Multiples

A. Diviseurs d'un nombre

1)

L'ensemble des diviseurs d'un nombres n se note div n.

Exemple : l'ensemble des diviseurs de 24 se note div 24

2)

Le nombre 1 divise tout nombre naturel.

Exemple : 1 divise 8 car 8 = 1 . 8

3)

Tout nombre naturel non nul est son plus grand diviseur.

Exemple : 9 divise 9, car 9 = 9 . 1

4)

0 "zéro" ne divise aucun nombre non nul.

Exemple : 0 ne divise pas 5, car il n'existe pas de nombre dont le produit par 0 soit 5.
Il est donc impossible de diviser par zéro.

B. Nombres particuliers

1)
 Nombre carrés
Un nombre carré possède un nombre impair de diviseurs.
Un nombre carré peut s'écrire sous la forme d'un produit de deux facteurs égaux.
Exemple :
 9 est un nombre carré car 9 possède 3 diviseurs : 1, 3, 9.
On peut écrire que 9 = 3 . 3 = 32
2)
 Nombres rectangles
Un nombres rectangle possède un nombre pair de diviseurs.
Exemple :
 6 est un nombre rectangle car 6 possède 4 diviseurs : 1, 2 , 3 ,6.
3)
 Nombres premiers
Un nombre est premier s'il admet que 2 diviseurs distincts.
Exemple :
 5 est un nombre premier car 5 ne possède que deux diviseurs distincts : 1 et 5
Contre exemple:
 1 n'est pas premier car il admet qu'un seul diviseur.

C. Multiples – Diviseurs

18 = 3 . 6 signifie que
 3 et 6 divisent 18.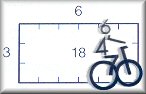    
3 et 6 sont des diviseurs de 18.
18 est divisible par 3 et 6.
18 est un multiple de 3 et 6.
   
a = b . c signifie que
b et c divisent a.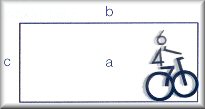    
b et c sont des diviseurs de a.
a est divisible par b et c.
a est multiple de b et de c.

D. Propriétés

1)

Si un nombre en divise deux autres, alors il divise leur somme.
Exemple :
 3 divise 60 et 9 alors il divise 69.

Formulation mathématique :

a, b, c étant des nombres naturels :
si a divise b et c, alors a divise b + c
2)

Si un nombre en divise deux autres, alors il divise leur différence.
Exemple :
 3 divise 60 et 9 alors il divise 51.

Formulation mathématique :

a, b, c étant des nombres naturels :
si a divise b et c, alors a divise b – c
(avec b plus grand que c ou b>c)
3)

Si un nombre en divise un autre, alors il divise tous les multiples de cet autre.

Exemple :
 5 divise 10 alors 5 divise tous les multiple de 10 (20, 30, 40, ...)

Formulation mathématique :

a, b, nétant des nombres naturels :
si a divise b, alors a divise b . n

E. Caractères de divisibilité

1)

Un nombre est divisible par 2 si son dernier chiffre est pair.
2)

Un nombre est divisible par 5 si son dernier chiffre est 5 ou 0.
3)

Un nombre est divisible par 4 si ses deux derniers chiffres forment un nombre divisible par 4.
4)
 Un nombre est divisible par 25 si ses deux derniers chiffres forment un nombre divisible par 25.
5)
 Un nombre est divisible par 8 si ses trois derniers chiffres forment un nombre divisible par 8.
6)
 Un nombre est divisible par 125 si ses trois derniers chiffres forment un nombre divisible par 125.
7)
 Un nombre est divisible par 3 si la somme de ses chiffres est un nombre divisible par 3.
8)
 Un nombre est divisible par 9 si la somme de ses chiffres est un nombre divisible par 9.

Vos remarques sont les bienvenues.